ElGamal
The ElGamal Encryption Scheme is an asymmetric key encryption algorithm for public key cryptography algorithm for public key cryptography and it is based on Diffie Helman key exchange.Key generation
- Randomly choose a secret key x with 1 < x < p − 1.
- Compute y = g x mod p.
- The public key is (p, g, y).
- The secret key is x.
These steps are performed once by the signer.
These steps are performed once by the signer.
Signature generation
To sign a message m the signer performs the following steps.
- Choose a random k such that 1 < k < p − 1 and gcd(k, p − 1) = 1.
- Compute
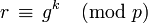 .
.
- Compute
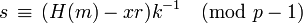 .
.
- If
 start over again.
start over again.
Then the pair (r,s) is the digital signature of m. The signer repeats these steps for every signature.
To sign a message m the signer performs the following steps.
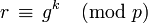 .
.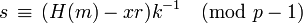 .
. start over again.
start over again.
Then the pair (r,s) is the digital signature of m. The signer repeats these steps for every signature.
Verification
A signature (r,s) of a message m is verified as follows.
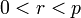 and
and 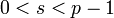 .
.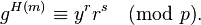
The verifier accepts a signature if all conditions are satisfied and rejects it otherwise.
A signature (r,s) of a message m is verified as follows.
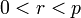 and
and 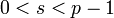 .
.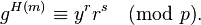
The verifier accepts a signature if all conditions are satisfied and rejects it otherwise.
Batch verification approach
In modified version of ElGamal Batch verification approach, multiplication of 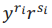 is computed for a batch of r and s. Then get the summation of collision-resistant hash value for every message and checks for the equality of both values of summation of hash and the multiplication of
is computed for a batch of r and s. Then get the summation of collision-resistant hash value for every message and checks for the equality of both values of summation of hash and the multiplication of 
A signature (r,s) of a message m is verified as follows.
and
.
The verification scheme accepts a signatures if all conditions are satisfied and rejects if there exists at least one forged signature.



No comments:
Post a Comment